第６節 分析技法
第４項 統計学メモ
|
(1)理論負荷性 (2)統計の入手 (3)正規分布と偏差値 (4)サンプル調査 (5)多変量解析 |
(1)理論負荷性
地域を知るためには、まず現地を見て回り、いろいろな人から話を聞き、さらに多様な資料に目を通すことが肝要である。しかし、見聞を広めるだけでは事例的事実の収集に留まり、自らの先入観に都合のいい事例を並べがちとなる(これは「理論負荷性」と言われている)。また、他地域と比較した相対的な位置付などを含めた確実な知識には至り難い。
そこで、いろいろな見聞を踏まえつつも、統計的な指標の検討が必要となる。
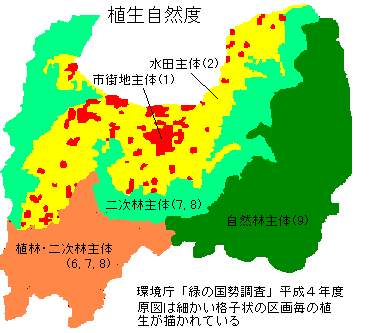理論負荷性の事例富山県は自然が豊かだという先入観があるが、日常の居住空間の自然は乏しい。
(2)統計の入手
インターネットを利用して多様な統計が利用できるようになっている。日本の統計は、「政府統計の総合窓口」。
各国の統計はもとより世界銀行など国際機関の統計サイトも充実している。
(3)正規分布と偏差値
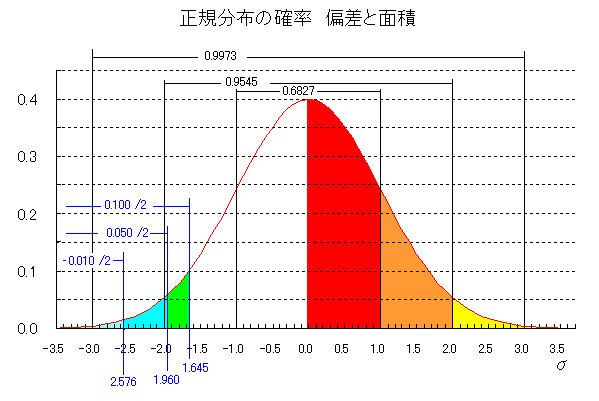
平均から乖離した指標を見つける手段となる。
偏差
＝各データと平均の差
分散
＝偏差平方の平均
標準偏差
＝分散の平方根
標準偏差(Standard Deviation) σ、s、ｄなどが記号として用いられる。
正規化；(各データ−平均値)/標準偏差
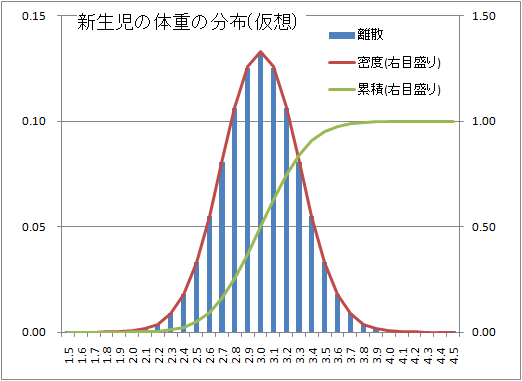赤ちゃんの体重は偏差値で表現すると分かり易い。体重を聞いてもその月令の赤ちゃんの平均的体重を知っている訳ではない。
2d以上大きい⇒上位2.3％に入っている。
(4)サンプル調査
統計には、比率を求める場合と平均値を求める場合がある。
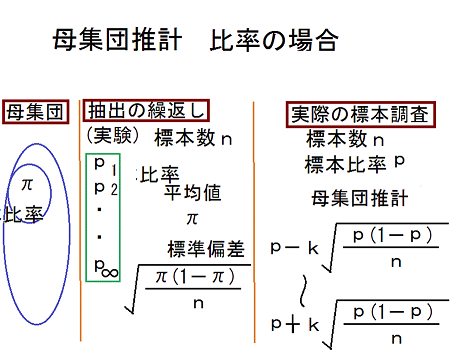
比率の場合
標本数(n)が小さいと、標準偏差が大きくなり、結果として求められる標本比率の幅が大きくなる。
実際の調査では標本抽出が偏っていることも多い。
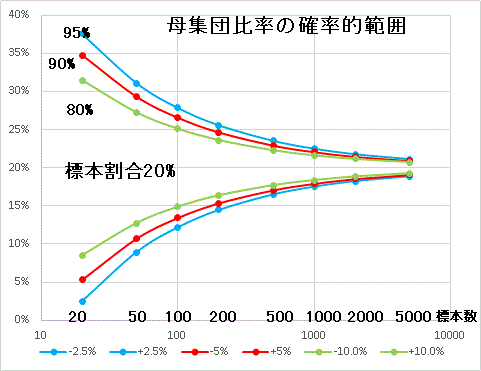p±√(p*(1-p)/n)の幅の中に68％入るp±1.96√(p*(1-p)/n)の幅の中に95％入る
平均値の場合(5)多変量解析
| 多変量解析法 | |||
| 外的基準 | 目的 | 量的データ | 質的データ |
| あり | 予測 | 回帰分析 | 数量化T類 |
| 判別 | 判別分析 | 数量化U類 | |
| なし | 分類 | クラスター分析 | 数量化V類 数量化W類 |
| 変数の合成 | 主成分分析 | ||
| 潜在因子の発見 | 因子分析 | ||
| これ以外にも多様な手法が考案されています。 | |||
都道府県の指標を多変量解析(クラスター分析、主成分分析、因子分析など)。
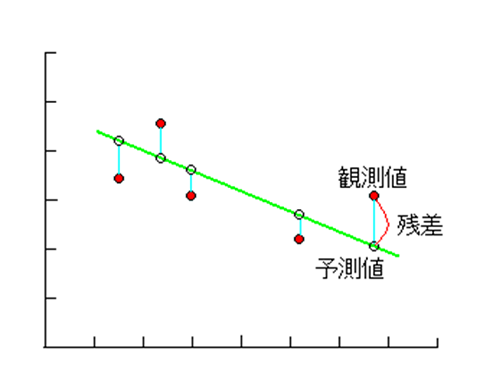
「回帰分析」
残差の分散(散らばりの程度)の元のデータの分散に対する比率が小さいほど相関は大きい。
相関係数の二乗
＝１−（残差分散−元データ分散）/元データ分散
| 生活 保護率 | 完全 失業率 | 世帯 規模 | 高齢化 比率 | 持ち家 率 | DID 人口 比率 | 社会 心理的 障壁 | ||
| 生活保護率(千人当たり) | 1.000 | |||||||
| 経済的環境 | 完全失業率 | 0.721 | 1.000 | |||||
| 生活支援 | 世帯規模 | -0.745 | -0.391 | 1.000 | ||||
| 経済的弱者 | 高齢化比率 | -0.133 | -0.378 | 0.159 | 1.000 | |||
| 生活費 | 持ち家率 | -0.670 | -0.578 | 0.711 | 0.640 | 1.000 | ||
| 都市的環境 | DID人口比率 | 0.537 | 0.548 | -0.585 | -0.660 | -0.753 | 1.000 | |
| 歴史的経緯 | 社会心理的障壁 | 0.421 | 0.285 | -0.309 | -0.060 | -0.329 | 0.240 | 1.000 |
| 生活保護率と高い相関がある | ||||||||
| 被説明変数との高い相関 | ||||||||
| 生活保護率=53.2+6.35*失業率-23.3*世帯規模 補正R2=0.76 | ||||||||
「相関行列」
関連する統計指標を並べ、相互の相関係数を求める。
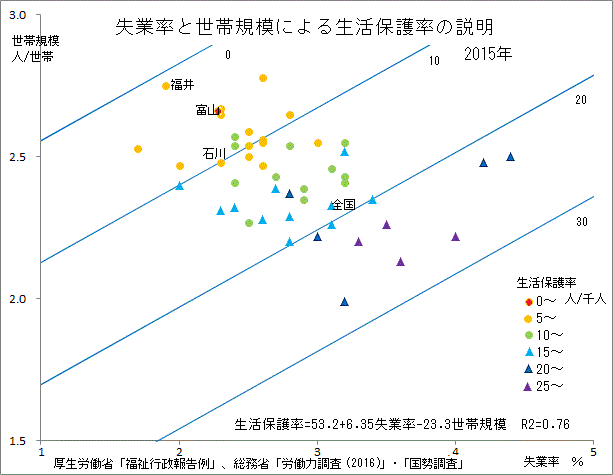説明力の高い複数の説明変数を取り出す。
因果関係図を描いてみる。相関係数が高いことが必ずしも因果関係の高さに繋がらないことに留意が必要。
「因子分析、主成分分析、クラスター分析」
因子分析は、データ内に潜む構造を見出す手法。主成分分析は、データから構造を作り出す手法。
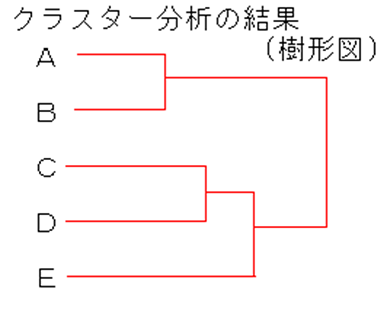クラスター分析は、関連の強いデータを順に繋いでいく手法。
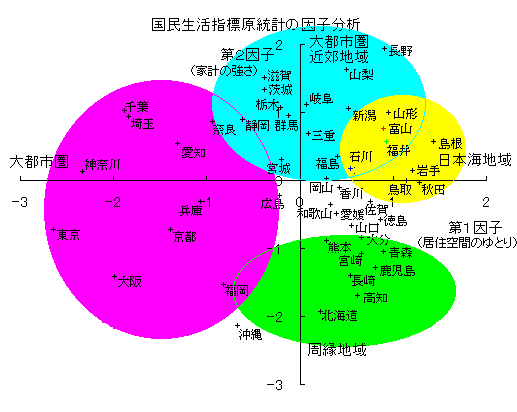都道府県統計の因子分析の例。日本海沿岸＝太平洋沿岸型軸及び中央＝周縁型の中央軸が見いだされる。
３つの分析は同じデータを利用しており、当然だが似た結果となる。
(Aug.23,2021)