就業構造による地域分析(多変量分析)
−モノづくり県富山−
多変量分析の手法は、かつては専ら理論的議論がなされ、実践的には、あまり活用されなかった。実際に利用しようとした場合、苦労が多く、その割には得るものが少なかったということであろう。社会科学の分野などでは、定番ソフトＳＰＳＳが次第に普及し、それなりに用いられてきている。ただし、そのソフトは高価(IBM-SPSSの一般版で189,000円、アカデミー版のサービス価格で約半額)であり、必ずしも気軽に利用できるソフトではない。
しかし、情報技術の進歩、普及の中で次第に容易に利用できるようになってきている。
例えば、以下は、主として、小椋將弘著「Excelで簡単多変量解析―データ入力一発解答(CD-ROM付)」講談社2006年(定価3990円)を使った分析である。このソフトは、機能は限定されるが、逆にデータを貼り付けさえすればExcelの再計算で自動的に結果がでるものとなっている(一部、指示に基づいて、行列式の計算等の補完入力が必要)。
また、Excelのアドインソフトとしてエスミ「EXCEL多変量解析ver5.0)」(定価39900円、ただし通販入手価格で27088円)などもある。
ただし、ソフトの計算の正しさに疑問を挟む向きもあり、ＳＰＳＳでないと、学会では認められないという都市伝説もあるそうだ。
いずれにしろ、このような状況の中で、幾つかの分析手法を試み、相互に比較検討することなども容易になっている。
主成分分析と因子分析
各産業の固有ベクトル・因子負荷量
以下では、国勢調査(2005年)の都道府県別就業者数(常住地ベース)の産業業種別構成比を用いて、都道府県の産業構造の捉え方を検討する。ただし、分析の都合上、零細な業種は類似業種と統合し、10業種として行った。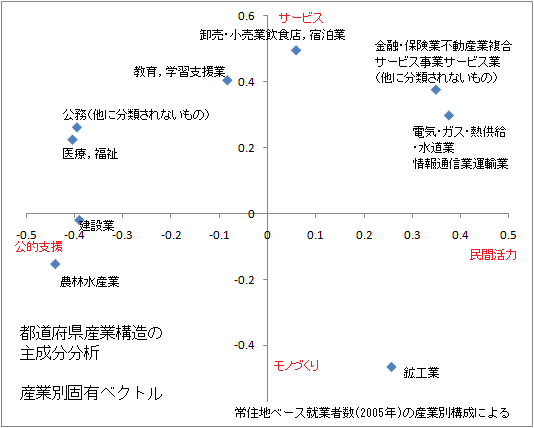
右図は、主成分分析を行い、業種の固有ベクトルを図示したものである。ここでの固有ベクトルの値は、各主成分での貢献度と呼べるものである。
まず、第一主成分(横軸)については、民間活力で自律している業種と公的支援を受けている業種の軸として捉えることができよう。
第二主成分(縦軸)については、サービス提供とモノづくりの軸として捉えることができよう。
第一軸、第二軸の全情報量に対する寄与率は、それぞれ44％、31％であり、産業構造を都道府県の角度から見た場合、民間活力と公的支援の軸が大きく現れることは興味深い。
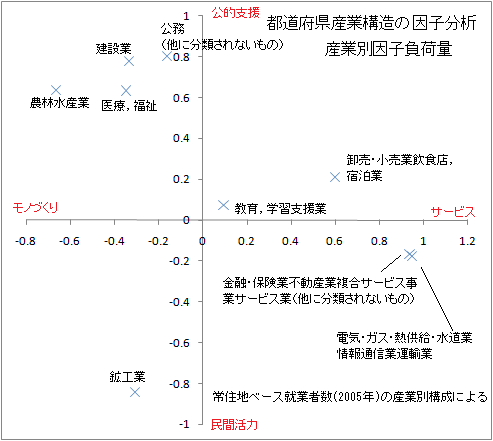次の右図は、因子分析を行い、業種の因子負荷量を図示したものである。これは、主成分分析の固有ベクトルと対応するものと考えてよいであろう。ここでの業種の配置は、実は、概ね、主成分分析での配置を90度回転させたものとなっている。
また、第一因子と第二因子の寄与率は、それぞれ39％、38％でほとんど差がない。
結論として、各業種の位置付けは、主成分分析と因子分析と概ね同じ結果となっているといえよう。
各都道府県の主成分得点・因子得点
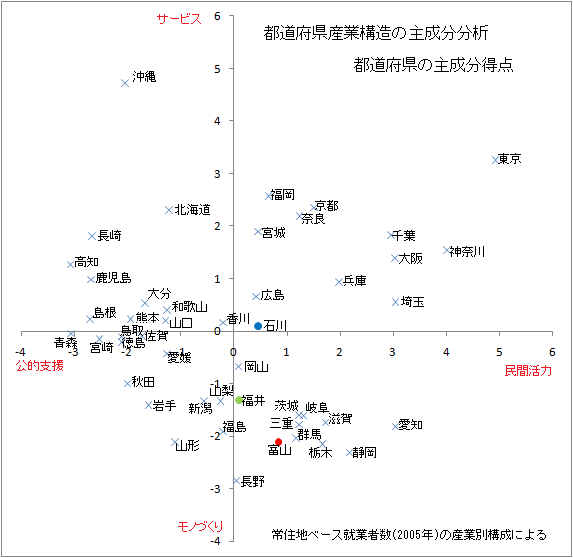次に、主成分分析での各都道府県の産業構造の位置付けについて見る。まず、東京等の都市圏では、民間活力で動き、サービス提供が卓越する地域となっている。
これに対して、富山などを含む、本州中央部で大都市圏以外の地域(愛知を含む)では、民間活力で動き、モノづくりが卓越する地域となっている。
他方、その他は、公的支援に依存する地域となるが、東北地方等は、モノづくりに傾斜し、沖縄・九州や北海道はサービスに傾斜している。
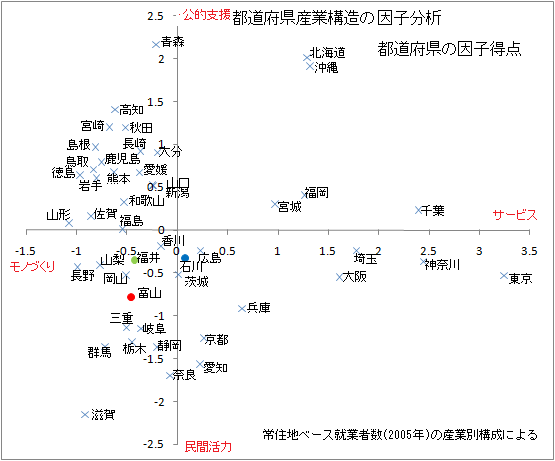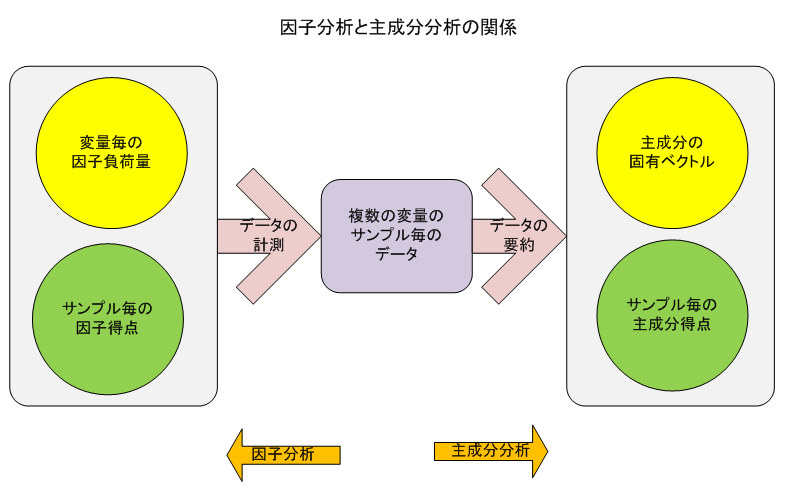
因子分析での各都道府県の産業構造の位置付けは、図での配置は回転しているが、概ね主成分分析と見合うものとなっている。下図は、主成分分析と因子分析の関連性を整理したものである。
我々が観測できる統計値は、それぞれの各サンプル(都道府県)が持つ業種別因子得点と各業種の因子負荷量の積和として現れたものと想定し、因子分析は、これを元に戻って探り出そうとする分析手法である。
他方、主成分分析では、多数の観測値の要約を目指して、各サンプル(都道府県)の主成分得点と各業種の固有ベクトル(値)の積和として表現したものである。
このような考え方での２つの分析が、理論的に一致するという訳ではないが、内容が似通ったものとなることは、十分にあり得る。私自身の経験では、実際に類似したものが求められている。
実は、考え方の理屈はともかく、２つの分析は、同じものを求めようとしているのではなかろうか。
このような考え方に至れば、敢えて因子の存在を想定する因子分析に対して、主成分分析の方が潔く、分析手法も明快で好ましいように思える。
こうした言説は、因子分析の理論の美しさを思いやる人からは、非難されることであろう。
クラスター分析との比較
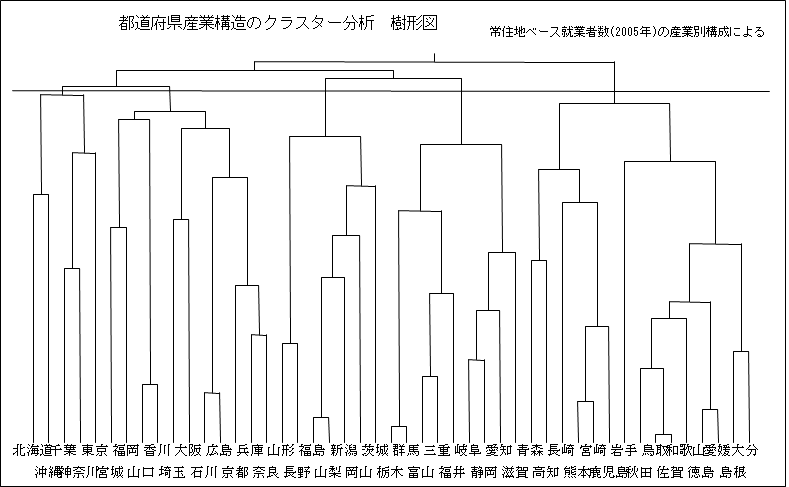
下図は、都道府県別就業者数(常住地ベース)の産業業種別構成比についてクラスター分析を行い、樹形図として表したものである。
|
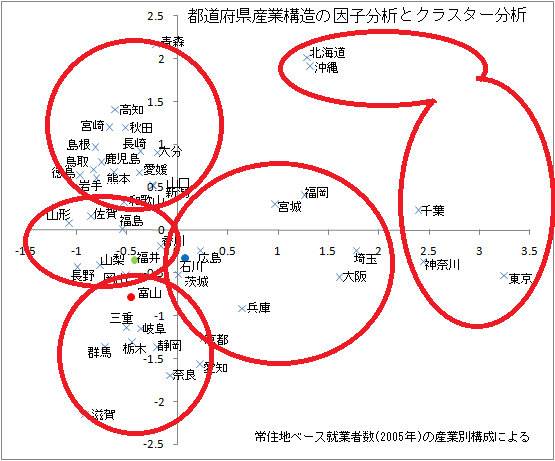右図は、各クラスターを上述の因子分析の都道府県の配置図上に描いたものである。当然の結果ではあるが、２つの分析は整合性があるといえよう。なお、北海道・沖縄と東京などが属するグルーブについては、因子分析の図上では、若干無理な描写となっているが、このグルーブは、クラスターを６つ増やした場合に、分割されるものである。 以上、主成分分析、因子分析、クラスター分析を小生なりに整理すると、このような統計の分析にあたっては、一般には、「主成分分析をまず行い、グルーピングをクラスター分析で補完する」ことを基本とすればよいのではなかろうか。 (統計データ) 関連項目に戻る (Sep.07,2010) |